Modeling the dynamic viscosity of Newtonian Fluids using the Eyring’s Theory and the Residual Helmholtz Free Energy

Modelación de la viscosidad dinámica de fluidos newtonianos a partir de la teoría de Eyring y la energía libre de Helmholtz residual

Published 2022-06-01

Modelación de la viscosidad dinámica de Fluidos Newtonianos a partir de la Teoría de Eyring y la Energía Libre de Helmholtz Residual
Open | Download
pdf (Spanish) FLIP
Issue
Vol. 19 No. 38 (2022): Table of contents Revista EIA No. 38
Section
Articles
How to Cite
Modeling the dynamic viscosity of Newtonian Fluids using the Eyring’s Theory and the Residual Helmholtz Free Energy. (2022). Revista EIA, 19(38), 3809 pp. 1-16. https://doi.org/10.24050/reia.v19i38.1535
DOI

https://doi.org/10.24050/reia.v19i38.1535
Dimensions
PlumX
Citations
Crossref
Citations in Crossref
Scopus
Citations in Scopus
Google Scholar
Europe PMC
Citations in Europe PMC
license
Creative Commons License

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Copyright statement

The authors exclusively assign to the Universidad EIA, with the power to assign to third parties, all the exploitation rights that derive from the works that are accepted for publication in the Revista EIA, as well as in any product derived from it and, in in particular, those of reproduction, distribution, public communication (including interactive making available) and transformation (including adaptation, modification and, where appropriate, translation), for all types of exploitation (by way of example and not limitation : in paper, electronic, online, computer or audiovisual format, as well as in any other format, even for promotional or advertising purposes and / or for the production of derivative products), for a worldwide territorial scope and for the entire duration of the rights provided for in the current published text of the Intellectual Property Law. This assignment will be made by the authors without the right to any type of remuneration or compensation.

Consequently, the author may not publish or disseminate the works that are selected for publication in the Revista EIA, neither totally nor partially, nor authorize their publication to third parties, without the prior express authorization, requested and granted in writing, from the Univeridad EIA.

Luis Fernando Cardona Palacio
Universidad Católica Luis Amigó
https://orcid.org/0000-0002-6526-9508
Show authors biography

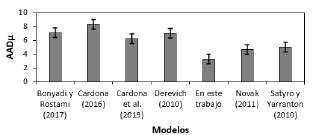
In this work, the dynamic viscosity of Newtonian fluids is modeled using Eyring's theory and the residual Helmholtz free energy. In order to estimate this energy, a modified Peng-Robinson cubic equation of state is applied. The adjustable parameters of the model have been determined from experimental data in the liquid and vapor coexistence for n-alkanes and n-alcohols. Later these parameters have been generalized using simple mathematical expressions that depend on the molecular weight of each substance. The predictive capabilities of the model are evaluated under single-phase conditions. The absolute deviations during correlation are below 3.27% while in prediction are below 5.60%. The generalized model is extended to mixtures using a simple mixture rule with one binary interaction parameter and the result without interaction is 8.19% and estimated is 3.45%. Finally, the model is compared with others in the literature and the statistical results show that the generalized model provides acceptable results.

Article visits 859 | PDF visits 447

Downloads

Download data is not yet available.
  1. Assael, M. J.; Charitidou, E.; Dymond, J. H.; Papadaki, M. (1992). Viscosity and thermal conductivity of binary n-heptane+ n-alkane mixtures. International journal of thermophysics, 13(2), 237-249. https://doi.org/10.1007/BF00504434
  2. Abdulagatov, I. M.; Azizov, N. D. (2006). (p, ρ, T, x) and viscosity measurements of {x1n-heptane+(1− x1) n-octane} mixtures at high temperatures and high pressures. The Journal of Chemical Thermodynamics, 38(11), 1402-1415. https://doi.org/10.1016/j.jct.2006.01.012
  3. Benabithe, Z. Z.; Vanegas, D.; Montoya, J. C. R.; Velásquez, J. A. (2020). Caso de estudio de la destilación etanol-agua en operación continua y discontinua y su simulación con ecuaciones cúbicas de estado y modelos de actividad. TecnoLógicas, 23(49), 223-249. https://doi.org/10.22430/22565337.1638
  4. Bonyadi, M.; Rostami, M. (2017). A new viscosity model based on Soave-Redlich-Kwong equation of state. Fluid Phase Equilibria, 451, 40-47. https://doi.org/10.1016/j.fluid.2017.07.009
  5. Bloxham, J. C.; Redd, M. E.; Giles, N. F.; Knotts IV, T. A.; Wilding, W. V. (2021). Proper Use of the DIPPR 801 Database for Creation of Models, Methods, and Processes. Journal of Chemical & Engineering Data, 66(1), 3-10. https://doi.org/10.1021/acs.jced.0c00641
  6. Cardona, L. F. (2016). Calculation of the viscosity of hydrocarbons based on the cubic equation of state of Jarrahian-Heidaryan. Revista Mexicana De Ingeniería Química, 15(3), 1019-1025.
  7. Cano-Gómez, J. J.; Iglesias-Silva, G. A.; Castrejón-González, E. O.; Ramos-Estrada, M.; Hall, K. R. (2015). Density and viscosity of binary liquid mixtures of ethanol+ 1-hexanol and ethanol+ 1-heptanol from (293.15 to 328.15) K at 0.1 MPa. Journal of
  8. Chemical & Engineering Data, 60(7), 1945-1955. https://doi.org/10.1021/je501133u
  9. Cardona, L. F.; Forero, L. A.; Velásquez, J. A. (2019). Modelamiento de la Viscosidad con Base en una Ecuación Cúbica μTP del Tipo Peng-Robinson. Información tecnológica, 30(4), 259-272. http://dx.doi.org/10.4067/S0718-07642019000400259
  10. Chevalier, J. L. E.; Petrino, P. J.; Gaston-Bonhomme, Y. H. (1990). Viscosity and density of some aliphatic, cyclic, and aromatic hydrocarbons binary liquid mixtures. Journal of Chemical and Engineering Data, 35(2), 206-212. https://doi.org/10.1021/je00060a034
  11. Daubert, T. E. (1998). Evaluated equation forms for correlating thermodynamic and transport properties with temperature. Industrial & Engineering Chemistry Research, 37(8), 3260-3267. https://doi.org/10.1021/ie9708687
  12. Derevich, I. V. (2010). Thermodynamic model of viscosity of hydrocarbons and their mixtures. International Journal of Heat and Mass Transfer, 53(19-20), 3823-3830. https://doi.org/10.1016/j.ijheatmasstransfer.2010.04.035
  13. Elliott, J. R.; Lira, C. T.; Lira, C. T. (2012). Introductory chemical engineering thermodynamics (2a ed.). Nueva York: Prentice Hall.
  14. Fan, T. B.; Wang, L. S. (2006). A viscosity model based on Peng-Robinson equation of state for light hydrocarbon liquids and gases. Fluid Phase Equilibria, 247(1-2), 59-69. https://doi.org/10.1016/j.fluid.2006.06.008
  15. Forero, L. A.; Velásquez, J. A. (2019). Representación Simultánea del Equilibrio Líquido-Vapor, el Volumen Molar y la Entalpía de Exceso de Mezclas Complejas mediante una Ecuación de Estado tipo Peng-Robinson. Información Tecnológica, 30(6), 21-34. http://dx.doi.org/10.4067/S0718-07642019000600021
  16. Hussein, N. M.; Asfour, A. F. A. (2009). Densities and kinematic viscosities of ten binary 1-alkanol liquid systems at temperatures of (293.15 and 298.15) K. Journal of Chemical & Engineering Data, 54(10), 2948-2952. https://doi.org/10.1021/je800497u
  17. Kontogeorgis, G. M.; Folas, G. K. (2010). Thermodynamic models for industrial applications: from classical and advanced mixing rules to association theories. Nueva York: John Wiley & Sons, Inc.
  18. Kumagai, A.; Yokoyama, C. (1998). Liquid viscosity of binary mixtures of methanol with ethanol and 1-propanol from 273.15 to 333.15 K. International Journal of Thermophysics, 19(1), 3-13. https://doi.org/10.1023/A:1021438800094
  19. Lasdon, L. S.; Waren, A. D.; Jain, A., Ratner, M. (1978). Design and testing of a generalized reduced gradient code for nonlinear programming. ACM Transactions on Mathematical Software, 4(1), 34-50. https://doi.org/10.1145/355769.355773
  20. Lemmon, E. W.; Huber, M. L.M.; Mclinden, M. O. (2007). NIST standard reference database 23: reference fluid thermodynamic and transport properties-REFPROP. (version 8.0) [software]. NIST-REFPROP 8. https://www.nist.gov/publications/nist-standard-reference-database-23-reference-fluid-thermodynamic-and-transport-0?pub_id=50520
  21. Liu, X.; Zhu, C.; He, M.; Zhang, Y. (2017). Correlation for viscosities of pure liquids at high pressures. Journal of Molecular Liquids, 231, 404-410. https://doi.org/10.1016/j.molliq.2017.02.026
  22. Martins, R. J.; Cardoso, M. J. D. M.; Barcia, O. E. (2003). A new model for calculating the viscosity of pure liquids at high pressures. Industrial & Engineering Chemistry Research, 42(16), 3824-3830. https://doi.org/10.1021/ie021017o
  23. Novak, L. T. (2011). Fluid viscosity-residual entropy correlation. International Journal of Chemical Reactor Engineering, 9(1), 1-27. https://doi.org/10.2202/1542-6580.2839
  24. Poulopoulos, S. G.; Philippopoulos, C. J. (2003). The effect of adding oxygenated compounds to gasoline on automotive exhaust emissions. J. Eng. Gas Turbines Power, 125(1), 344-350. https://doi.org/10.1115/1.1501076
  25. Poling, B. E.; Prausnitz, J. M.; O’connell, J. P. (2001). Properties of gases and liquids (5a ed.). Nueva York: McGraw-Hill Education.
  26. Sastry, N. V.; Raj, M. M. (1996). Densities, speeds of sound, viscosities, dielectric constants, and refractive indices for 1-heptanol+ hexane and+ heptane at 303.15 and 313.15 K. Journal of Chemical & Engineering Data, 41(3), 612-618. https://doi.org/10.1021/je950172p
  27. Sastry, N. V.; Valand, M. K. (1998). Densities, viscosities, and relative permittivities for pentane+ 1-alcohols (C1 to C12) at 298.15 K. Journal of Chemical & Engineering Data, 43(2), 152-157. https://doi.org/10.1021/je9701801
  28. Satyro, M. A.; Yarranton, H. W. (2010). Expanded fluid-based viscosity correlation for hydrocarbons using an equation of state. Fluid Phase Equilibria, 298(1), 1-11. https://doi.org/10.1016/j.fluid.2010.06.023
  29. Valderrama, J. O. (2003). The state of the cubic equations of state. Industrial & Engineering Chemistry Research, 42(8), 1603-1618. https://doi.org/10.1021/ie020447b
  30. Valderrama, J. O.; Muñoz, J. M.; Rojas, R. E. (2011). Viscosity of ionic liquids using the concept of mass connectivity and artificial neural networks. Korean Journal of Chemical Engineering, 28(6), 1451-1457. https://doi.org/10.1007/s11814-010-0512-0
  31. Varzandeh, F.; Stenby, E. H.; Yan, W. (2017). General approach to characterizing reservoir fluids for EoS models using a large PVT database. Fluid Phase Equilibria, 433, 97-111. https://doi.org/10.1016/j.fluid.2016.10.018
  32. Valderrama, J. O.; Cardona, L. F.; Rojas, R. E. (2019). Correlation and prediction of ionic liquid viscosity using Valderrama-Patel-Teja cubic equation of state and the geometric similitude concept. Part I: pure ionic liquids. Fluid Phase Equilibria, 497, 164-177. https://doi.org/10.1016/j.fluid.2019.04.034

Information

Sistema OJS 3.4.0.7 - Metabiblioteca |