Computational fluid dynamics simulation in cone-bottom stirred tanks with a Rushton and pitchedblade turbines

Simulación dinámica computacional en tanques agitados de fondo cónico con turbina Rushton y de palas inclinadas

Published 2023-12-19

Open | Download
PDF (Spanish) FLIP
Issue
Vol. 20 No. 40 (2023): Table of contents Revista EIA No. 40
Section
Articles
How to Cite
Computational fluid dynamics simulation in cone-bottom stirred tanks with a Rushton and pitchedblade turbines. (2023). Revista EIA, 20(40), 4010 pp. 1-22. https://doi.org/10.24050/reia.v20i40.1676
DOI

https://doi.org/10.24050/reia.v20i40.1676
Dimensions
PlumX
Citations
Crossref
Citations in Crossref
Scopus
Citations in Scopus
Google Scholar
Europe PMC
Citations in Europe PMC
license
Creative Commons License

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Copyright statement

The authors exclusively assign to the Universidad EIA, with the power to assign to third parties, all the exploitation rights that derive from the works that are accepted for publication in the Revista EIA, as well as in any product derived from it and, in in particular, those of reproduction, distribution, public communication (including interactive making available) and transformation (including adaptation, modification and, where appropriate, translation), for all types of exploitation (by way of example and not limitation : in paper, electronic, online, computer or audiovisual format, as well as in any other format, even for promotional or advertising purposes and / or for the production of derivative products), for a worldwide territorial scope and for the entire duration of the rights provided for in the current published text of the Intellectual Property Law. This assignment will be made by the authors without the right to any type of remuneration or compensation.

Consequently, the author may not publish or disseminate the works that are selected for publication in the Revista EIA, neither totally nor partially, nor authorize their publication to third parties, without the prior express authorization, requested and granted in writing, from the Univeridad EIA.

Luis Fernando Cardona Palacio
Universidad Católica Luis Amigó - Colombia
https://orcid.org/0000-0002-6526-9508
Juan E. Arismendy
Universidad Pontificia Bolivariana - Colombia
German Camilo Quintana Marín
Universidad Pontificia Bolivariana - Colombia
Hader Humberto Alzate Gil
Universidad Pontificia Bolivariana - Colombia
Diego A. Hincapié
Instituto Tecnológico Metropolitano - Colombia
Show authors biography

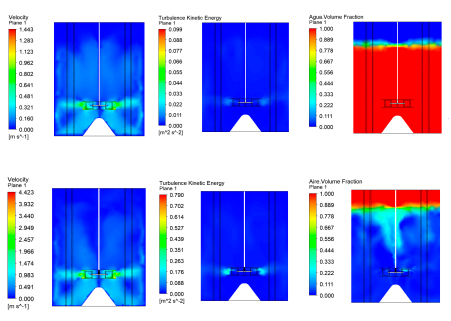
Computational Fluid Dynamics (CFD) is a tool frequently used for the optimization
and improvement of industrial processes. In this work, the CFD simulation is used for
analyzing the appropriate power in stirred-tank systems with three different types of cones
at the bottom of the tank and with two types of impellers: 45° pitch 4- bladed turbine (axial
impeller) and Rushton standard turbine (radial impeller). The simulation was carried out in
a stirred tank with a diameter of 27 cm and with different cone diameters and height ratios
are analyzed. Also, 4 rotation speeds (50, 100, 300, and 600 rpm) were evaluated to describe
the transition to turbulent states. Reynolds Stress Model (RSM) and the Moving Reference
Frame are used. The results show that the power decrease with the axial impeller when
this is operated at low Reynolds number values meanwhile the radial impeller presented an
increase in the values of power when the cone is introduced inside the tank. By increasing
the Reynolds number an exponential increase in the power volume of each impeller is
made. Also, the inclusion of a 4-impeller blade inclination between laminar and transition
shows a significant saving in power consumption and for turbulent regimes, the inclusion
of geometries in the bottom of the tank affects power consumption. Finally, the results are
validated using experimental data and show that the absolute deviations are below 4 %.

Article visits 371 | PDF visits 206

Downloads

Download data is not yet available.
  1. ANSYS. (2009a). Reynolds stress model [Online]. https://www.sharcnet.ca/Software/Fluent12/html/th/node79.htm (Accessed: 20 May 2022)
  2. ANSYS. (2009b). Standard k-ε - Model. [Online]. https://www.sharcnet.ca/Software/Fluent12/html/th/node58.htm (Accessed: 20 May 2022)
  3. Chudacek, M. W. (1985). Suspension in profiled mixing. Chemical Engineering Science, 40(3), pp. 385–392 https://doi.org/10.1016/0009-2509(85)85100-9
  4. Coroneo, M.; Montante, G.; Paglianti, A.; Magelli, F. (2011). CFD prediction of fluid flow and mixing in stirred tanks: Numerical issues about the RANS simulations. Computers and Chemical Engineering, 35(10), pp. 1959–1968 https://doi.org/10.1016/j.compchemeng.2010.12.007
  5. Daubert, T. E. (1998). Evaluated equation forms for correlating thermodynamic and transport properties with temperature. Industrial & Engineering Chemistry Research, 37(8), pp. 3260-3267 https://doi.org/10.1021/ie9708687
  6. Delgadillo, J. A.; Rajamani, R. K. (2005). A comparative study of three turbulence-closure models for the hydrocyclone problem. International Journal of Mineral Processing, 77(4), pp. 217–230 https://doi.org/10.1016/j.minpro.2005.06.007
  7. Dong, J.; Hu, B.; W Pacek, A.; Yang, X.; Miles, N. (2016). The Effect of Bottom Shape and Baffle Length on the Flow in Stirred Tanks in Turbulent and Transitional Flow. International Academy of Mechanical and Mechatronic Engineering, 10(9), pp. 1644–1653 https://doi.org/10.5281/zenodo.1126537
  8. Guha, D.; Ramachandran, P. A.; Dudukovic, M. P.; Derksen, J. J. (2008). Evaluation of Large Eddy Simulation and Euler-Euler CFD for Solids Flow Dynamics in a Stirred Tank Reactor. American Institute of Chemical Engineers AIChE, 54(3), pp. 766–788 https://doi.org/10.1002/aic.11417
  9. Joshi, J. B.; Nere, N. K.; Rane, C. V.; Murthy, B. N.; Mathpati, C. S.; Patwardhan, A. W.; Ranade, V. V. (2011a). CFD simulation of stirred tanks: Comparison of turbulence models. Part I: Radial flow impellers. Canadian Journal of Chemical Engineering, 89(1), pp. 23–82 https://doi.org/10.1002/cjce.20446
  10. Joshi, J. B.; Nere, N. K.; Rane, C. V.; Murthy, B. N.; Mathpati, C. S.; Patwardhan, A. W.; Ranade, V. V. (2011b). CFD simulation of stirred tanks: Comparison of turbulence models (Part II: Axial flow impellers, multiple impellers and multiphase dispersions). Canadian Journal of Chemical Engineering, 89(4), pp. 754–816 https://doi.org/10.1002/cjce.20465
  11. Lane, G. L.; Koh, P. T. L. (1997). CFD Simulation of a Rushton Turbine in a Baffled Tank, International Conference on Computational Fluid Dynamics in Mineral & Metal Processing and Power Generation. Clayton South, Victoria, Australia, pp. 377-386. https://www.cfd.com.au/cfd_conf97/papers/lan035.pdf
  12. Li, L.; Chen, N.; Xiang, K.; Xiang, B. (2018). CFD simulation of hydrodynamics characteristics in a tank stirred by a hollow self‐inducing impeller. Canadian Journal of Chemical Engineering, 96(8), pp. 1-12 https://doi.org/10.1002/cjce.23135
  13. Martínez, F. M.; Valencia, A. (2010). Estudio numérico de la fluidodinámica de un estanque de agitación utilizando método de mallas deslizantes (Tesis de pregrado en Ingeniería Civil), Chile, Facultad de Ciencias Físicas y Matemáticas Departamento de
  14. Ingeniería Mecánica, Chile, p. 90. https://repositorio.uchile.cl/handle/2250/103931
  15. McCabe, W. L.; Smith, J. C.; Harriot, P. (2007). Operaciones Unitarias En Ingeniería Química. McGraw Hill, pp. 260-281.
  16. Micale, G.; Montante, G.; Grisafi, F.; Brucato, A.; Godfrey, J. (2000). CFD Simulation of Particle Distribution in Stirred Vessels. Chemical Engineering Research and Design, 78(3), pp. 435-444 https://doi.org/10.1205/026387600527338
  17. Montante, G.; Lee, K. C.; Brucato, A.; Yianneskis, M. (2001). Numerical simulations of the dependency of flow pattern on impeller clearance in stirred vessels. Chemical Engineering Science, 56(12), pp. 3751-3770 https://doi.org/10.1016/S0009-2509(01)00089-6
  18. Motamedvaziri, S.; Armenante, P. M. (2012). Flow regimes and surface air entrainment in partially filled stirred vessels for different fill ratios. Chemical Engineering Science, 81, pp. 231–250 https://doi.org/10.1016/j.ces.2012.05.050
  19. Naeeni, S. K.; Pakzad, L. (2019). Droplet size distribution and mixing hydrodynamics in a liquid–liquid stirred tank by CFD modeling. International Journal of Multiphase Flow, 120, p. 103100 https://doi.org/10.1016/j.ijmultiphaseflow.2019.103100
  20. Ochieng, A., & Onyango, M. S. (2008). Homogenization energy in a stirred tank. Chemical Engineering and Processing: Process Intensification, 47(9-10), pp. 1853-1860. https://doi.org/10.1016/j.cep.2007.10.014
  21. Ochieng, A.; Onyango, M. S.; Kumar, A.; Kiriamiti, K.; Musonge, P. (2008). Mixing in a tank stirred by a Rushton turbine at a low clearance. Chemical Engineering and Processing: Process Intensification, 47(5), pp. 842-851 https://doi.org/10.1016/j.cep.2007.01.034
  22. Paul, E. L.; Atiemo-Obeng, V. A.; Kresta, S. M. (2004). Handbook of industrial mixing, New Jersey, John Wiley & Sons, Inc., pp. 359-375.
  23. Pukkella, A. K.; Vysyaraju, R.; Tammishetti, V.; Rai, B.; Subramanian, S. (2019). Improved mixing of solid suspensions in stirred tanks with interface baffles: CFD simulation and experimental validation. Chemical Engineering Journal, 358, pp. 621–633 https://doi.org/10.1016/j.cej.2018.10.020
  24. Sheikhi, N.; Najafi, M.; Enjilela, V. (2020). Modifying a meshless method to solving κ− ε turbulent natural convection heat transfer. International Journal of Modern Physics C, 31(01), p. 2050014 https://doi.org/10.1142/S012918312050014X
  25. Versteeg, H. K.; Malalasekera, W. (1995). An Introduction to Computational Fluid Dynamics: The volume finite method (1st ed.), London, Pearson education, pp. 1-40.
  26. Wu, H.; Patterson, G. K. (1989). Laser-Doppler measurements of turbulent-flow parameters in a stirred mixer. Chemical Engineering Science, 44(10), pp. 2207–2221 https://doi.org/10.1016/0009-2509(89)85155-3
  27. Wutz, J.; Waterkotte, B.; Heitmann, K.; Wucherpfennig, T. (2020). Computational fluid dynamics (CFD) as a tool for industrial UF/DF tank optimization. Biochemical Engineering Journal, 160, p. 107617 https://doi.org/10.1016/j.bej.2020.107617

Information

Sistema OJS 3.4.0.7 - Metabiblioteca |