Vibration control of seismicly excited structures using a device with inerter system

Control de vibración de estructuras excitadas sísmicamente usando un dispositivo con sistema inerter

Published 2024-01-01

Open | Download
PDF (Spanish) FLIP
Issue
Vol. 21 No. 41 (2024): Tabla de contenido Revista EIA No. 41
Section
Articles
How to Cite
Vibration control of seismicly excited structures using a device with inerter system. (2024). Revista EIA, 21(41), 4110 pp. 1-25. https://doi.org/10.24050/reia.v21i41.1685
DOI

https://doi.org/10.24050/reia.v21i41.1685
Dimensions
PlumX
Citations
Crossref
Citations in Crossref
Scopus
Citations in Scopus
Google Scholar
Europe PMC
Citations in Europe PMC
license
Creative Commons License

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Copyright statement

The authors exclusively assign to the Universidad EIA, with the power to assign to third parties, all the exploitation rights that derive from the works that are accepted for publication in the Revista EIA, as well as in any product derived from it and, in in particular, those of reproduction, distribution, public communication (including interactive making available) and transformation (including adaptation, modification and, where appropriate, translation), for all types of exploitation (by way of example and not limitation : in paper, electronic, online, computer or audiovisual format, as well as in any other format, even for promotional or advertising purposes and / or for the production of derivative products), for a worldwide territorial scope and for the entire duration of the rights provided for in the current published text of the Intellectual Property Law. This assignment will be made by the authors without the right to any type of remuneration or compensation.

Consequently, the author may not publish or disseminate the works that are selected for publication in the Revista EIA, neither totally nor partially, nor authorize their publication to third parties, without the prior express authorization, requested and granted in writing, from the Univeridad EIA.

John Jairo Blandón Valencia
Universidad Nacional de Colombia - Sede Medellín
https://orcid.org/0000-0003-3229-6910
Daniel Alejandro Caicedo
University of Minho, Portugal
Luis Augusto Lara Valencia
Universidad Nacional de Colombia
Show authors biography

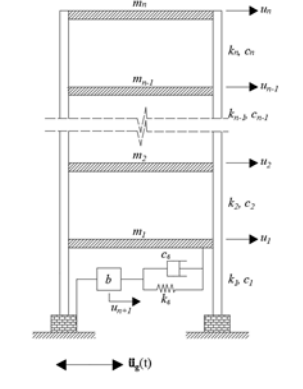
An important part of the structural design process is to decrease the effect of
vibration in buildings, particularly those that may be subject to seismic excitation.
Although research in the field of structural control has been made since the early
1900s, the complexity and dimensions of civil structures make this problem
particularly difficult to solve due to the high demand for control effort and many
other associated limitations. This paper analyzes the performance of a novel
passive control system that can be used for vibration control in civil structures
subjected to base excitation. This control device is called Tuned Inerter Damper
(TID), which overcomes the limitation of classic passive devices that are efficient in
a narrow frequency band for which they are tuned, a situation that is inconvenient
since earthquakes exhibit a very diverse frequency content on most occasions.
Besides, this study employs a metaheuristic optimization approach based on the
differential evolution method (DE) combined with an elastic time-history dynamic
analysis, through which the vibration control focuses on two individual objectives:
first, minimizing the maximum horizontal displacement; and second, minimizing
the root mean square (RMS) response of displacements. A 12-story building
equipped with a novel arrangement of the TID, and subjected to multiple seismic
excitations is studied to verify the effectiveness of the device. The results show a
significant enhancement in the dynamic response when the arrangement presented
in this work is used, and considerably better than an equivalent TMD. Therefore,
TID represents a potentially attractive alternative to traditional passive control
techniques.

Article visits 290 | PDF visits 168

Downloads

Download data is not yet available.
  1. Pan, C., & Zhang, R. (2018). Design of structure with inerter system based on stochastic response mitigation ratio. Structural Control and Health Monitoring, 25(6). doi:https://doi.org/10.1002/stc.2169
  2. Bekdaş, G., & Nigdeli, S. M. (2011). Estimating optimum parameters of tuned mass dampers using harmony search. Engineering Structures, 33(9), 2716-2723. doi:http://dx.doi.org/10.1016/j.engstruct.2011.05.024
  3. BekdaşG, Nigdeli, S. M., & Yang, X. S. (2018). A novel bat algorithm based optimum tuning of mass dampers for improving the seismic safety of structures. Engineering Structures, 159, 89-98. doi:http://dx.doi.org/10.1016/j.engstruct.2017.12.037
  4. Biswas Raha, S., & Chakraborty, N. (2012). Tuned reactive power dispatch through modified differential evolution technique. Frontiers in Energy, 6, 138-147. doi:http://dx.doi.org/10.1007/s11708-012-0188-8
  5. Buckle, G. (2000). Passive control of structures for seismic loads. Bull. N.Z. Natl. Soc. Earthq. Eng, 33(3), 209-221. doi:https://doi.org/10.5459/bnzsee.33.3.209-221.
  6. Bureerat, S., & Pholdee, N. (2017). Adaptive sine cosine algorithm integrated with differential evolution for structural damage detection. Computational Science and Its Applications–ICCSA 2017: 17th International Conference, 71-86. doi:http://dx.doi.org/10.1007/978-3-319-62392-4_6
  7. Chen, Y. C., Tu, J. Y., & Wang, F. V. (2015). Earthquake vibration control for buildings with inerter networks. 2015 European Control Conference (ECC), 3137-3142. doi:http://dx.doi.org/10.1109/ECC.2015.7331016
  8. Den Hartog, J. P. (1985). Mechanical vibrations. New York: Courier Corporation.
  9. Farshidianfar, A., & Soheili, S. (2013). Optimization of TMD parameters for earthquake vibrations of tall buildings including soil structure interaction. Iran University of Science & Technology, 3(3), 409-429.
  10. Frahm, H. (1911). Device for damping vibrations of bodies. U.S. Pat. No 989,958, 1911. doi:https://doi.org/10.1016/j.tree.2005.10.010
  11. Hu, Y., & Chen, M. Z. (2015). Performance evaluation for inerter-based dynamic vibration absorbers. Int. J. Mech. Sci, 99, 297-307. doi:https://doi.org/10.1016/j.ijmecsci.2015.06.003
  12. Inc, T. M. (2019). MATLAB R2019a. MA, USA: Natick.
  13. Kelly, J. M. (1998). Base isolation: Origins and development. EERC News, 12(1).
  14. Kelly, J. M., & Beucke, K. E. (1983). A frictional damped base isolation system with fail-safe characteristics. Earthq. Eng. Struct. Dynam, 11, 33-56.
  15. Kelly, J. M., & Hodder, S. B. (1982). Experimental study of lead and elastomeric dampers for base isolation system in laminated neoprene bearings. Bull. N.Z. Nat. Soc. Earthq. Eng, 15, 53-67.
  16. Lazar, I. F., Neild, S. A., & Wagg, D. J. (2014). Design and performance analysis of inerter-based vibration control systems. Dynamics of Civil Structures, 4, 493-500. doi:http://dx.doi.org/10.1007/978-3-319-04546-7_53
  17. Lazar, I. F., Neild, S. A., & Wagg, D. J. (2014). Using an inerter‐based device for structural vibration suppression. Earthq. Eng. Struct. Dyn, 43(8), 1129-1147. doi:https://doi.org/10.1002/eqe.2390
  18. Lazar, I. F., Wagg, D. J., & Neild, S. A. (2013). An inerter vibration isolation system for the control of seismically excited structures. 10th International Conference on Urban Earthquake Engineering.
  19. Lazar, I., Neild, S., & Wagg, D. (2014). Inerter-based Vibration Suppression Systems for Laterally and Base-Excited Structures. (E. C. A. Cunha, Ed.) Proceedings of the 9th International Conference on Structural Dynamics.
  20. Leung, A. Y., & Zhang, H. (2009). Particle swarm optimization of tuned mass dampers. Engineering Structures, 31(3), 715-728. doi:http://dx.doi.org/10.1016/j.engstruct.2008.11.017
  21. Ministerio de Vivienda, C. y. (2010). Reglamento Colombiano de Construcción Sismo Resistente NSR-10. Bogotá: AIS.
  22. Nigdeli, S. M., Bekdas, G., & Yang, X. S. (2016). Optimum tuning of mass dampers for seismic structures using flower pollination algorithm. Int. J. Theor. Appl. Mech, 1, 264-268.
  23. Ormondroyd, J., & Den Hartong, J. P. (1928). The theory of the dynamic vibration absorber. Transaction of the ASME, 50, 9-22.
  24. Papageorgiou, C., & Smith, M. (2005). Laboratory experimental testing of inerters. Proceedings of the 44th IEEE Conference on Decision and Control, and the European Control Conference. doi:https://doi.org/10.1109/CDC.2005.1582679
  25. Said, E. (2018). Seismic Energy Assessment of Buildings with Tuned Vibration Absorbers. Shock and Vibration, 2018, 1-10. doi:https://doi.org/10.1155/2018/2051687
  26. Seyedpoor, S. M., Shahbandeh, S., & Yazdanpanah, O. (2015). An efficient method for structural damage detection using a differential evolution algorithm-based optimisation approach. Civil Engineering and Environmental Systems, 32(3), 230-250. doi:http://dx.doi.org/10.1080/10286608.2015.1046051
  27. Shen, W., Niyitangamahoro, A., Feng, Z., & Zhu, H. (2019). Tuned Inerter Dampers for Civil Structures Subjected to Earthquake Ground Motions: optimum design and seismic performance. Engineering Structures, 198. doi:https://doi.org/10.1016/j.engstruct.2019.109470
  28. Shen, Y., Chen, L., Yang, X., Shi, D., & Yang, J. (2016). Improved design of dynamic vibration absorber by using the inerter and its application in vehicle suspension. Journal of Sound and Vibration(361), 148-158. doi:http://dx.doi.org/10.1016/j.jsv.2015.06.045
  29. Smith, M. (2002). Synthesis of mechanical networks: The inerter. IEEE Transactions on automatic control, 47(10), 1648-1662. doi:https://doi.org/10.1109/TAC.2002.803532
  30. Storn, R., & Price, K. (1997). Differential Evolution - A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Global Optim, 11(4), 341-359. doi:https://doi.org/10.1023/A:1008202821328.
  31. Vo-Duy, T., Ho-Huu, V., Dang-Trung, H., & Nguyen-Thoi, T. (2016). A two-step approach for damage detection in laminated composite structures using modal strain energy method and an improved differential evolution algorithm. Composite Structures, 147, 42-53. doi:http://dx.doi.org/10.1016/j.compstruct.2016.03.027
  32. Wang, F. C., Chen, C. W., Liao, M. K., & Hong, M. F. (2007). Performance analyses of building suspension control with inerters. 46th IEEE Conference on Decision and Control, 3786-3791.
  33. Wang, F. C., Hong, M. F., & Chen, C. W. (2010). Building suspensions with inerters. Proceedings of the Institution of Mechanical Engineers, Part C. J. Mech. Eng. Sci, 224(8), 1605-1616. doi:https://doi.org/10.1243/09544062JMES1909.
  34. Wen, Y., Chen, Z., & Hua, X. (2017). Design and evaluation of tuned inerter-based dampers for the seismic control of MDOF structures. Journal of Structural Engineering, 143(4). doi:http://dx.doi.org/10.1061/(ASCE)ST.1943-541X.0001680
  35. Yucel, M., Bekdaş, G., Nigdeli, S. M., & Sevgen, S. (2019). Estimation of optimum tuned mass damper parameters via machine learning. Journal of Building Engineering, 26.

Information

Sistema OJS 3.4.0.7 - Metabiblioteca |