Total tardiness optimization on parallel machines: case study in the coffee industry

Optimización de la tardanza total en máquinas paralelas: caso de estudio en la industria del café

Published 2024-01-01

Open | Download
PDF (Spanish) FLIP
Issue
Vol. 21 No. 41 (2024): Tabla de contenido Revista EIA No. 41
Section
Articles
How to Cite
Total tardiness optimization on parallel machines: case study in the coffee industry. (2024). Revista EIA, 21(41), 4102 pp. 1-20. https://doi.org/10.24050/reia.v21i41.1710
DOI

https://doi.org/10.24050/reia.v21i41.1710
Dimensions
PlumX
Citations
Crossref
Citations in Crossref
Scopus
Citations in Scopus
Google Scholar
Europe PMC
Citations in Europe PMC
license
Creative Commons License

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Copyright statement

The authors exclusively assign to the Universidad EIA, with the power to assign to third parties, all the exploitation rights that derive from the works that are accepted for publication in the Revista EIA, as well as in any product derived from it and, in in particular, those of reproduction, distribution, public communication (including interactive making available) and transformation (including adaptation, modification and, where appropriate, translation), for all types of exploitation (by way of example and not limitation : in paper, electronic, online, computer or audiovisual format, as well as in any other format, even for promotional or advertising purposes and / or for the production of derivative products), for a worldwide territorial scope and for the entire duration of the rights provided for in the current published text of the Intellectual Property Law. This assignment will be made by the authors without the right to any type of remuneration or compensation.

Consequently, the author may not publish or disseminate the works that are selected for publication in the Revista EIA, neither totally nor partially, nor authorize their publication to third parties, without the prior express authorization, requested and granted in writing, from the Univeridad EIA.

Alejandro Uribe
Universidad EAFIT
Santiago López Duque
Universidad EAFIT
Juan Pablo Mesa López
Universidad EAFIT
Jose Alejandro Montoya Echeverry
Universidad EAFIT
Show authors biography

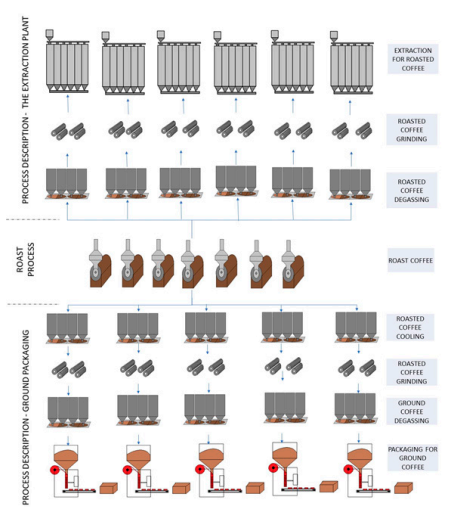
Production scheduling is one of the most important tasks in manufacturing systems since it allows the allocation of jobs with a certain number of available resources. In the production and service industries, meeting the established commitments with the different customers and production deadlines can lead to higher levels of satisfaction and market competitive advantages. On the other hand, one of the main industries worldwide is the coffee industry. Indeed, coffee is the second most traded commodity in the world. Therefore, this research addresses the optimization of the total tardiness in the scheduling of jobs in parallel machines for a case study in a coffee roaster. This is an NP-hard problem where each job requires the roasting process and, in addition, has an associated delivery time. Each job’s processing time depends on the machine that is designated and not all machines can run all jobs. We present the mathematical model to describe the problem using mixed integer linear programming and then it is implemented in Python. Additionally, a mate heuristic model based on the ATC heuristic is proposed in order to reduce the computation time and to reach solutions close to the optimum. This model was evaluated with one thousand instances of real data from the roasting process. The Gurobi optimizer was used to solve the problem. The exact method shows high computational times, so we proposed to first perform the sequencing of jobs and then assign them to the machines by means of a simplified mathematical model. By using the proposed mate heuristic model, an average reduction of 53.98% of the execution time is achieved and with respect to the solution delay, this model achieves a median of 0.0% with respect to the optimum.

Article visits 291 | PDF visits 239

Downloads

Download data is not yet available.
  1. Azizoǧlu, M.; & Kirca, Ö. (1998). Tardiness minimization on parallel machines. International Journal of Production Economics, 55(2), 163-168. https://doi.org/10.1016/s0925-5273(98)00034-6.
  2. Bektur, G.; & Saraç, T. (2019). A mathematical model and heuristic algorithms for an unrelated parallel machine scheduling problem with sequence-dependent setup times, machine eligibility restrictions and a common server. Computers & Operations Research, 103, 46-63. https://doi.org/10.1016/j.cor.2018.10.010
  3. Berthier, A.; Yalaoui, A.; Chehade, H.; Yalaoui, F.; Yalaoui, F.; & Bouillot, C. (2022). Unrelated parallel machines scheduling with dependent setup times in textile industry. Computers & Industrial Engineering, 174, 108736. https://doi.org/10.1016/j.cie.2022.108736
  4. Costa, A. S.; Alves, R. C.; Vinha, A. F.; Barreira, S. V. P.; Nunes, M. A.; Cunha, L. M.; & Oliveira, M. B. P. (2014). Optimization of antioxidants extraction from coffee silverskin, a roasting by-product, having in view a sustainable process. Industrial Crops and Products, 53, 350-357. https://doi.org/10.1016/j.indcrop.2014.01.006
  5. Diana, R. O. M.; De Souza, S. R.; & Filho, M. F. F. (2018). A variable neighborhood descent as ILS local search to the minimization of the total weighted tardiness on unrelated parallel machines and sequence dependent setup times. Electronic Notes in Discrete Mathematics, 66, 191-198. https://doi.org/10.1016/j.endm.2018.03.025
  6. Fang, W.; Zhu, H.; & Mei, Y. (2022). Hybrid meta-heuristics for the unrelated parallel machine scheduling problem with setup times. Knowledge-Based Systems 241:108193. https://doi.org/10.1016/j.knosys.2022.108193.
  7. Heydar, M.; Mardaneh, E.; & Loxton, R. (2022). Approximate dynamic programming for an energy-efficient parallel machine scheduling problem. European Journal of Operational Research 302(1):363–80. https://doi.org/10.1016/j.ejor.2021.12.041
  8. Lenstra, J. K.; & Vakhania, N. (2023). On the complexity of scheduling unrelated parallel machines with limited preemptions.Operations Research Letters 51(2):187–89. https://doi.org/10.1016/j.orl.2023.02.004.
  9. Li, K.; Shi, Y.; Yang, S.; & Cheng, B. (2011). Parallel machine scheduling problem to minimize the makespan with resource dependent processing times. Applied Soft Computing 11(8):5551–57. https://doi.org/10.1016/j.asoc.2011.05.005.
  10. Monch, L. (2008). Heuristics to Minimize Total Weighted Tardiness of Jobs on Unrelated Parallel Machines. 2008 IEEE International Conference on Automation Science and Engineering 572–77. doi: 10.1109/COASE.2008.4626531.
  11. Ratanasanya, S.; Chindapan, N.; Polvichai, J.; Sirinaovakul, B.; & Devahastin, S. (2022). Model-based optimization of coffee roasting process: model development, prediction, optimization and application to upgrading of robusta coffee beans. Journal of Food Engineering 318:110888. doi: https://doi.org/10.1016/j.jfoodeng.2021.110888.
  12. Ruíz, R.; García-Díaz, J. C.; & Álvarez, C. M. (2007). Considering scheduling and preventive maintenance in the flowshop sequencing problem. Computers & Operations Research 34(11):3314–30. doi: https://doi.org/10.1016/j.cor.2005.12.007.
  13. Sanati, H.; Moslehi, G.; & Reisi‐Nafchi, M. (2023). Unrelated parallel machine energy-efficient scheduling considering sequence-dependent setup times and time-of-use electricity tariffs. EURO Journal on Computational Optimization 11:100052. doi: https://doi.org/10.1016/j.ejco.2022.100052.
  14. Tanaka, S.; & Araki, M. (2008). A branch-and-bound algorithm with lagrangian relaxation to minimize total tardiness on identical parallel machines. International Journal of Production Economics 113(1):446–58. doi: https://doi.org/10.1016/j.ijpe.2007.10.006.
  15. Vincent, B. G.; Duhamel, C.; Ren, L.; & Tchernev, N. (2016). An efficient heuristic for scheduling on identical parallel machines to minimize total tardiness. IFAC-PapersOnLine 49(12):1737–42. https://doi.org/10.1016/j.ifacol.2016.07.833
  16. Wang, B.; Feng, K.; & Wang, X. (2023). Bi-objective scenario-guided swarm intelligent algorithms based on reinforcement learning for robust unrelated parallel machines scheduling with setup times. Swarm and Evolutionary Computation 80:101321. https://doi.org/10.1016/j.swevo.2023.101321
  17. Wang, H.; Li, R.; & Gong, W. (2023). Minimizing tardiness and makeSpan for distributed heterogeneous unrelated parallel machine scheduling by knowledge and Pareto-based memetic algorithm. Egyptian Informatics Journal 24(3):100383. https://doi.org/10.1016/j.eij.2023.05.008
  18. Wang, S.; Wu, R.; Chu, F.; & Yu, J. (2023). An exact decomposition method for unrelated parallel machine scheduling with order acceptance and setup times. Computers & Industrial Engineering 175:108899. https://doi.org/10.1016/j.cie.2022.108899
  19. Yalaoui, F.; & Chen, C. (2002). Parallel machine scheduling to minimize total tardiness. International Journal of Production Economics 76(3):265–79. https://doi.org/10.1016/S0925-5273(01)00175-X
  20. Zhao, Y.; Xu, X.; Xu, E.; & Niu, B. (2021). Stochastic customer order scheduling on heterogeneous parallel machines with resource allocation consideration. Computers & Industrial Engineering 160:107539. https://doi.org/10.1016/j.cie.2021.107539

Information

Sistema OJS 3.4.0.7 - Metabiblioteca |